How accurate is DFT in theory and in practice? There has been some reviews on the former, comparing calculations of a given DFT program with experiments, but not as much of the latter – comparing the numerical approximations inherent in different DFT codes. I came across a paper taking both of these aspects into account. The paper is titled “Error Estimates for Solid-State Density-Functional Theory Predictions: An Overview by Means of the Ground-State Elemental Crystals”, written by K. Lejaeghere et al. More information about their project to compare DFT codes can be found at their page at the Center for Molecular Modeling at the University of Gent.
Their approach to compare DFT codes is to look at the root mean square error of the equations of state w.r.t. the ones from Wien2K. They called this number the “delta-factor”. The sample set is the ground-state crystal structures of the elements H-Rn in the periodic table. I have plotted the outcome below, which is to be interpreted as the deviation from a full-potential APW+lo calculation, which is considered as the exact solution. Please note the logarithmic scale on the horizontal axis.
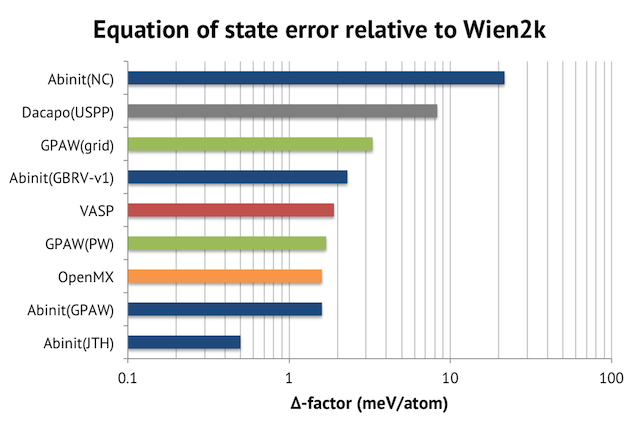
My observations are:
- Well-converged PAW calculations with good atomic setups are very accurate. Abinit with the JTH library achieves a delta value of 0.5 meV/atom vs Wien2K. As the authors put it in the paper: “predictions by APW+lo and PAW are for practical purposes identical”.
- Norm-conserving pseudopotentials (NC) with plane-wave basis set are an order of magnitude worse than PAW. The numerical error is of the same magnitude as the intrinsic error vs experiments for the PBE exchange-correlation potential (23.5 meV/atom).
- VASP is no longer the most accurate PAW solution. Similar, or better, quality results can now be arrived at with Abinit and GPAW.
- The quality of the PAW atomic setups matters a lot. Compare the results for Abinit (blue bars in the graph) with different PAW libraries. I think this explains why VASP has remained so popular – only recently did PAW-libraries which surpass VASP’s built-in one become available.
- The PAW setups for GPAW are of comparable quality to VASP’s, but GPAW’s grid approach seems to be detrimental to numerical precision. GPAW with plane-wave (PW) basis gets 1.7 meV/atom vs 3.3 meV/atom using finite differences.
- OpenMX (pseudo-atomic orbitals + norm-conserving PPs) performs surprisingly well, matching the PAW results. I noticed that the calculations employed very large basis sets, though, which should slow down the speed significantly.
Another relevant aspect is the relative speed of the different codes. Do you have to trade speed for precision? The paper does not mention the accumulated runtime for the different data sets, which would otherwise have made an interesting “price/performance” analysis possible.
Before, I tried to compare the absolute performance and the parallel caling of Abinit and VASP, reaching the conclusion that Abinit was significant slower. Perhaps the improved precision is the reason why? Regarding GPAW, I know, from unpublished results, that GPAW exhibits similar parallel scaling to VASP and matches the per core performance, but SCF convergence can be an issue. OpenMX can be extremely fast compared to plane-wave codes, but the final outcome critically depends on the choice of the basis set.
I am putting GPAW and OpenMX on my list of codes to benchmark this year.

