A2 OOOOOO DO EIIR Bettan
Följande variabelnamn är ej tillåtna under Fortran 77 (för långa
och/eller innehåller understrykningstecken) men väl under Fortran 90:
GUSTAVUS ADOLFUS GUSTAV_ADOLF
HEJ_DU_GLADE GOETEBORG
ABCDEFGHIJKLMNOPQRSTUVWXYZ
Följande variabelnamn är inte tillåtna under Fortran 77 och inte heller under
Fortran 90:
2C inleds av siffra 2_CESAR inleds av siffra ÅKE ej tillåtet med Å $KE ej tillåtet med $ C-B ej tillåtet med minustecken (men korrekt som uttryck) DOLLAR$ ej tillåtet med $ K**2 ej tillåtet med * (men korrekt som uttryck) _STOCKHOLM_ ej tillåtet med inledande _ (understrykningstecken)(3.2) Denna uppgift återkommer som övning (22.13).
(3.3) Denna uppgift återkommer som övning (22.12).
(3.4) En rekursiv variant av denna funktion finns i avsnittet 5.2.1.3. Här följer i stället en konventionell beräkning av fakulteten utnyttjande en DO-slinga.
PROGRAM HELTALS_FAKULTET
IMPLICIT NONE
INTEGER :: N
INTEGER, EXTERNAL :: FAK
WRITE(*,*) ' Heltalsberäkning av fakulteten'
DO
WRITE(*,*) ' Ge önskat värde på argumentet'
READ(*,*) N
IF (N < 0 ) EXIT
WRITE(*,*) ' För N = ', N, &
' blir fakulteten = ', FAK(N)
END DO
END PROGRAM HELTALS_FAKULTET
INTEGER FUNCTION FAK(N)
IMPLICIT NONE
INTEGER :: N, I
FAK = 1
IF (N < 0 ) THEN
WRITE(*,*) ' FELAKTIGT VÄRDE PÅ ARGUMENTET'
STOP
ELSE IF (N > 1 ) THEN
! Både N = 0 och 1 ger här fakulteten 1
DO I = 2, N
FAK = I*FAK
END DO
END IF
END FUNCTION FAK
På en "normal" dator med 32 bitars heltal blir 10! korrekt uträknat till 3 628 800,
men 13! blir felaktigt 1 932 053 504. Att detta är fel inses av att 13! måste ha minst
lika många nollor på slutet som 10! Man får dock inte rätt värde
genom att lägga till två nollor, siffrorna stämmer inte. Nästa värde
14! blir uträknat mindre än det felaktiga på 13!, och 17! blir negativ. Dessa
problem beror på att heltals-spill (eng. integer overflow) normalt ej signaleras, utan beräkningen
bara fortsätter.
PROGRAM FLYTTALS_FAKULTET
IMPLICIT NONE
REAL :: N
REAL, EXTERNAL :: FAK
WRITE(*,*) ' Flyttalsberäkning av fakulteten'
DO
WRITE(*,*) ' Ge önskat värde på argumentet'
READ(*,*) N
IF (N < 0.0 ) EXIT
WRITE(*,*) ' För N = ', N, &
' blir fakulteten = ', FAK(N)
END DO
END PROGRAM FLYTTALS_FAKULTET
REAL FUNCTION FAK(N)
IMPLICIT NONE
REAL :: N
INTEGER :: I
FAK = 1.0
IF (N < 0.0 ) THEN
WRITE(*,*) ' FELAKTIGT VÄRDE PÅ ARGUMENTET'
STOP
ELSE IF (N > 1.0 ) THEN
! Både N = 0 och 1 ger här fakulteten 1
DO I = 2, NINT(N) ! Avrundning
FAK = REAL(I)*FAK
END DO
END IF
END FUNCTION FAK
På en "normal" dator med IEEE aritmetik och enkel precision blir 10! korrekt uträknat
till 3,628800·10+6, medan 13! blir 6,2270208·10+9. Man får vidare 34! approximativt lika med
2,9523282·10+38, medan 35! ger spill. Detta beror på att flyttals-spill (eng. real overflow)
normalt signaleras, och att beräkningen avbrytes då. Flyttal är därför
säkrare att arbeta med än heltal i fall som detta.
PROGRAM SINUS
! TABELLERING AV SINUS-FUNKTIONEN
IMPLICIT NONE
DOUBLE PRECISION :: A, B, H, X
INTEGER :: N, I
INTRINSIC SIN
1 WRITE(*,*) ' Ge önskat intervall och antal delintervall!'
READ(*,*) A, B, N
IF ( A > B .OR. N <= 0 ) GO TO 1
H = (B - A)/DBLE(N)
WRITE(*,*)
WRITE(*,*) ' Tabellering av sinus-funktionen sin(x) '
WRITE(*,*)
WRITE(*,*) ' x sin(x)'
WRITE(*,*)
DO I = 0, N
X = A + DBLE(I)*H
WRITE(*,20) X, SIN(X)
END DO
20 FORMAT(1X,F12.6,F26.16)
WRITE(*,*)
STOP
END
Som synes valde jag att göra denna beräkning i dubbel precision. Körning med
enkla indata gav följande resultat.
Ge önskat intervall och antal delintervall!
0 1 10
Tabellering av sinus-funktionen sin(x)
x sin(x)
0.000000 0.0000000000000000
0.100000 0.0998334166468282
0.200000 0.1986693307950612
0.300000 0.2955202066613396
0.400000 0.3894183423086505
0.500000 0.4794255386042030
0.600000 0.5646424733950354
0.700000 0.6442176872376911
0.800000 0.7173560908995228
0.900000 0.7833269096274834
1.000000 0.8414709848078965
(3.7)
PROGRAM ETTAN
! Kontroll av de trigonometriska funktionerna SIN och COS
IMPLICIT NONE
REAL :: A, B, H, X
REAL :: Y, Z, ETTA, MAXFEL
INTEGER :: N, I
INTRINSIC SIN, COS
1 WRITE(*,*) ' Ge önskat intervall och antal delintervall!'
READ(*,*) A, B, N
IF ( A > B .OR. N <= 0 ) GO TO 1
H = (B - A)/REAL(N)
WRITE(*,*)
WRITE(*,*) ' Beräkning av felet vid beräkning av ', &
' sinus och cosinus'
WRITE(*,*)
MAXFEL = 0.0
DO I = 0, N
X = A + REAL(I)*H
Y = SIN(X)
Z = COS(X)
ETTA = Y**2 + Z**2
MAXFEL = MAX(MAXFEL, ABS(ETTA-1.0))
END DO
WRITE(*,20) MAXFEL
20 FORMAT(1X,E14.6)
WRITE(*,*)
END PROGRAM ETTAN
Resultatet av beräkningen på Sun blev föga överraskande
2·my = 2·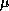 
= 0,1192·10-6.
(3.8) Denna uppgift återkommer som laboration 4 b. Någon lösning ges därför ej här.
(4.1) Detta är en mycket avancerad variant till lösning!
SUBROUTINE LOES_LIN_EKV_SYSTEM(A, X, B, FEL)
IMPLICIT NONE
! Fältdeklarationer
REAL, DIMENSION (:, :), INTENT (IN) :: A
REAL, DIMENSION (:), INTENT (OUT) :: X
REAL, DIMENSION (:), INTENT (IN) :: B
LOGICAL, INTENT (OUT) :: FEL
! Arbetsarean M är A utvidgad med B
REAL, DIMENSION (SIZE (B), SIZE (B) + 1) :: M
INTEGER, DIMENSION (1) :: MAX_LOC
REAL, DIMENSION (SIZE (B) + 1) :: TEMP_ROW
INTEGER :: N, K, I
! Initiera M
N = SIZE (B)
M (1:N, 1:N) = A
M (1:N, N+1) = B
! Triangulariseringsfas
FEL = .FALSE.
TRIANG_SLINGA: DO K = 1, N - 1
! Pivotering
MAX_LOC = MAXLOC (ABS (M (K:N, K)))
IF ( MAX_LOC(1) /= 1 ) THEN
TEMP_ROW (K:N+1 ) = M (K, K:N+1)
M (K, K:N+1)= M (K-1+MAX_LOC(1), K:N+1)
M (K-1+MAX_LOC(1), K:N+1) = TEMP_ROW( K:N+1)
END IF
IF (M (K, K) == 0) THEN
FEL = .TRUE. ! Singulär matris A
EXIT TRIANG_SLINGA
ELSE
TEMP_ROW (K+1:N) = M (K+1:N, K) / M (K, K)
DO I = K+1, N
M (I, K+1:N+1) = M (I, K+1:N+1) - &
TEMP_ROW (I) * M (K, K+1:N+1)
END DO
M (K+1:N, K) = 0 ! Dessa värden användes ej
END IF
END DO TRIANG_SLINGA
IF (M (N, N) == 0) FEL = .TRUE. ! Singulär matris A
! Återsubstitution
IF (FEL) THEN
X = 0.0
ELSE
DO K = N, 1, -1
X (K) = ( M (K, N+1) - &
SUM (M (K, K+1:N) * X (K+1:N)) ) / M (K, K)
END DO
END IF
END SUBROUTINE LOES_LIN_EKV_SYSTEM
Ingående matris A och vektorer B och X har
deklarerats med antaget mönster (assumed-shape
array), dvs typ, rang och namn ges här, medan omfånget ges i anropande rutin, och då
i ett explicit gränssnitt.
Notera att den inbyggda funktionen MAXLOC ger som resultat en heltalsvektor, med samma antal element som rangen (antalet dimensioner) hos argumentet. I vårt fall är argumentet en vektor, varför aktuell rang är ett och MAXLOC således ger en vektor med ett enda element. Detta är anledningen till att den lokala variabeln MAX_LOC deklarerats som en vektor med ett element. Om man deklarerar MAX_LOC som ett skalärt heltal fås kompileringsfel. Värdet blir naturligtvis index för det största elementet (det första av de största om flera är lika).
Notera även att numreringen börjar på 1 trots att jag tittar på en vektor med element som numreras från K till N. Jag har valt att inte utföra pivoteringen (dvs själva radbytet) om rutinen finner att raderna redan ligger rätt, nämligen när MAX_LOC(1) blir 1.
Beräkningen avbrytes så snart som singularitet konstateras, observera att denna kan inträffa så sent att den inte noteras inne i slingan.
Vid pivoteringen användes vektorn TEMP_ROW dels vid radbytet, dels utnyttjas den även för multiplikatorerna i Gausseliminationen.
Jag använder här tills vidare bara fältsektioner av vektortyp vid beräkningarna, men skall nu utnyttja funktionen SPREAD för att kunna använda fältsektioner av matristyp, varvid den innersta slingan försvinner (DO I = K+1, N).
Funktionen SPREAD (SOURCE, DIM, NCOPIES) returnerar ett fält av samma typ som argumentet SOURCE, men med rangen ökad med ett. Parametrarna DIM och NCOPIES är heltal. Om NCOPIES är negativ så användes i stället värdet noll. Om SOURCE är en skalär så blir SPREAD helt enkelt en vektor med NCOPIES element som alla har samma värde som SOURCE. Parametern DIM anger vilket index som skall utökas, det måste vara mellan 1 och 1+(rangen hos SOURCE), om SOURCE är en skalär måste således DIM vara ett. Parametern NCOPIES ger antalet element i den nya dimensionen, således ej antalet nya kopior. Om variabeln A svarar mot ett fält (/ 2, 3, 4 /) så blir
SPREAD (A, DIM=1, NCOPIES=3) SPREAD (A, DIM=2, NCOPIES=3)
2 3 4 2 2 2
2 3 4 3 3 3
2 3 4 4 4 4
Jag går nu över till fältsektioner av matristyp, vilka kan kompileras effektivare
på parallella maskiner, genom att byta ut den innersta explicita slingan, dvs
DO I = K+1, N
M (I, K+1:N+1) = M (I, K+1:N+1) - &
TEMP_ROW (I) * M (K, K+1:N+1)
END DO
mot
M (K+1:N, K+1:N+1) = M (K+1:N, K+1:N+1) &
- SPREAD( TEMP_ROW (K+1:N), 2, N-K+1) &
* SPREAD( M (K, K+1:N+1), 1, N-K)
Anledningen till att vi måste "krångla till" det med funktionen SPREAD är att
i den explicita slingan är (vid fixt I) variabeln TEMP_ROW(I) en konstant som multipliceras
med N-K+1 olika värden M. Å andra sidan användes samma vektor ur M för
alla värden på I, vilka är N-K stycken. Omformningen av matriserna skall ske
till två matriser med samma mönster som delmatrisen M (K+1:N, K+1:N+1), dvs N-K rader
och N-K+1 kolumner, eftersom alla de fyra räknesätten på fält är
element för element.
Det kan tyvärr vara litet besvärligt att få parametrarna till SPREAD helt rätt. Till hjälp kan vara att utnyttja funktionerna LBOUND och UBOUND för att få lägre och övre dimensioneringsgränser, liksom att skriva ut det nya fältet med satsen
WRITE(*,*) SPREAD(SOURCE,DIM,NCOPIES)
Notera då att utmatningen sker kolonnvis (dvs första index varierar snabbast, som vanligt
i Fortran). Man kan använda de lägre och övre dimensioneringsgränserna
för en mer explicit utmatningssats som ger en utmatning bättre anpassad till hur fältet
ser ut. Här måste man dock först ha gjort en tilldelning till ett vanligt deklarerat
fält med rätt mönster för att kunna utnyttja index på vanligt sätt.
Notera vidare att indexen i en konstruktion som SPREAD automatiskt kanar ner till 1 som lägre
gräns, även när man som SOURCE har något som A(4:7).
I den sista av DO-slingorna i programmet erhålles en tom summa vid index N, nämligen från N+1 till N. Enligt Fortrans regler blir denna summa noll, vilket är korrekt ur matematisk synpunkt. Om man har indexkontroll påslagen är det dock risk för att denna larmar. Jag har därför bytt ut
DO K = N, 1, -1
X (K) = ( M (K, N+1) - &
SUM (M (K, K+1:N) * X (K+1:N)) ) / M (K, K)
END DO
END IF
mot
X (N) = M (N, N+1) / M (N, N)
DO K = N-1, 1, -1
X (K) = ( M (K, N+1) - &
SUM (M (K, K+1:N) * X (K+1:N)) ) / M (K, K)
END DO
END IF
i programmet loes1.f90 i källkodsbiblioteket.
(5.1) Jag byter ut
IF ( F(MITT) > 0.0 ) THEN
V = MITT
ELSE
H = MITT
END IF
mot
IF ( F(MITT) == 0.0 ) THEN
NOLL = MITT
RETURN
ELSE IF ( F(MITT) > 0.0 ) THEN
V = MITT
ELSE
H = MITT
END IF
(5.2) En första ändring är att IF ( H - V >= EPS ) nu måste skrivas som
det fullständiga IF ( ABS(H - V) >= EPS ) eftersom vi inte längre kan vara säkra
på vilken punkt som är längst åt höger. En felutgång måste
läggas in för det fall att F(A) och F(B) har samma tecken. I testen IF ( F(MITT) > 0.0 ) byter vi ut F(MITT) mot F(MITT)*F(V).
(5.3) Om man vill använda en mer avancerad algoritm kan man byta ut satsen MITT = 0.5*(H-V), man kan därvid fortfarande kalla den nya punkten för MITT, trots att den nu inte längre ligger mitt mellan V och H.
RECURSIVE FUNCTION TRIBONACCI(N) RESULT (T_RESULTAT)
IMPLICIT NONE
INTEGER, INTENT(IN) :: N
INTEGER :: T_RESULTAT
IF ( N <= 3 ) THEN
T_RESULTAT = 1
ELSE
T_RESULTAT = TRIBONACCI(N-1) + &
TRIBONACCI(N-2) + TRIBONACCI(N-3)
END IF
END FUNCTION TRIBONACCI
Anropande program kan skrivas
IMPLICIT NONE
INTEGER :: N, M, TRIBONACCI
N = 1
DO
IF ( N <= 0 ) EXIT
WRITE (*,*) ' GE N '
READ(*,*) N
M = TRIBONACCI(N)
WRITE(*,*) N, M
END DO
END
och ger resultatet TRIBONACCI(15) = 2209.
(5.5) Filen kvad.f90 för adaptiv numerisk kvadratur (integration). Jag använder trapetsformeln, halverar steget och gör Richardsonextrapolation. Metoden blir därför ekvivalent med Simpsons formel. Som feluppskattning använder jag Linköpingsmodellen, där felet högst är beloppet av skillnaden mellan de båda icke extrapolerade värdena. Om felet är för stort tillämpas rutinen var för sig på de båda delintervallen, varvid tillåtet fel i vart och ett av delintervallen blir hälften av det tidigare tillåtna.
RECURSIVE FUNCTION ADAPTIV_KVAD (F, A, B, TOL, ABS_FEL) &
RESULT (RESULTAT)
IMPLICIT NONE
INTERFACE
FUNCTION F(X) RESULT (FUNKTIONSVAERDE)
REAL, INTENT(IN) :: X
REAL :: FUNKTIONSVAERDE
END FUNCTION F
END INTERFACE
REAL, INTENT(IN) :: A, B, TOL
REAL, INTENT(OUT) :: ABS_FEL
REAL :: RESULTAT
REAL :: STEG, MITT
REAL :: EN_TRAPETS_YTA, TVAA_TRAPETS_YTA
REAL :: VAENSTER_YTA, HOEGER_YTA
REAL :: DIFF, ABS_FEL_V, ABS_FEL_H
STEG = B - A
MITT = 0.5 * (A + B)
EN_TRAPETS_YTA = STEG * 0.5 * (F(A) + F(B))
TVAA_TRAPETS_YTA = STEG * 0.25 * (F(A) + F(MITT)) + &
STEG * 0.25 * (F(MITT) + F(B))
DIFF = TVAA_TRAPETS_YTA - EN_TRAPETS_YTA
IF ( ABS(DIFF) < TOL ) THEN
RESULTAT = TVAA_TRAPETS_YTA + DIFF/3.0
ABS_FEL = ABS(DIFF)
ELSE
VAENSTER_YTA = ADAPTIV_KVAD (F, A, MITT, &
0.5*TOL, ABS_FEL_V)
HOEGER_YTA = ADAPTIV_KVAD (F, MITT, B, &
0.5*TOL, ABS_FEL_H)
RESULTAT = VAENSTER_YTA + HOEGER_YTA
ABS_FEL = ABS_FEL_V + ABS_FEL_H
END IF
END FUNCTION ADAPTIV_KVAD
Filen test_kva.f90 för test av ovanstående rutin för adaptiv numerisk kvadratur
behöver INTERFACE både för funktionen F och för kvadraturrutinen ADAPTIV_KVAD.
Notera att för den senare måste funktionen F deklareras både med typ REAL och
med EXTERNAL.
Jag har valt att komplettera detta program med mätning av exekveringstiden, utnyttjande de i Fortran 90 inbyggda subrutinerna för detta, se Appendix 5, avsnitt 21.
PROGRAM TEST_ADAPTIV_KVAD
IMPLICIT NONE
INTERFACE
FUNCTION F(X) RESULT (FUNKTIONSVAERDE)
REAL, INTENT(IN) :: X
REAL :: FUNKTIONSVAERDE
END FUNCTION F
END INTERFACE
INTERFACE
RECURSIVE FUNCTION ADAPTIV_KVAD &
(F, A, B, TOL, ABS_FEL) RESULT (RESULTAT)
REAL, EXTERNAL :: F
REAL, INTENT(IN) :: A, B, TOL
REAL, INTENT(OUT) :: ABS_FEL
REAL :: RESULTAT
END FUNCTION ADAPTIV_KVAD
END INTERFACE
REAL :: A, B, TOL
REAL :: ABS_FEL
REAL :: RESULTAT, PI
INTEGER :: I
INTEGER :: COUNT1, COUNT2, COUNT_RATE
REAL :: TID
PI = 4.0 * ATAN(1.0)
A = -5.0 ; B = +5.0
TOL = 0.1
CALL SYSTEM_CLOCK(COUNT=COUNT1, COUNT_RATE=COUNT_RATE)
DO I = 1, 5
TOL = TOL/10.0
RESULTAT = ADAPTIV_KVAD (F, A, B, TOL, ABS_FEL)
WRITE(*,*)
WRITE(*,"(A, F15.10, A, F15.10)") &
"Integralen är approximativt ", &
RESULTAT, " med approximativ feluppskattning ", &
ABS_FEL
WRITE(*,"(A, F15.10, A, F15.10)") &
"Integralen är mer exakt ", &
SQRT(PI), " med verkligt fel ",&
RESULTAT - SQRT(PI)
END DO
CALL SYSTEM_CLOCK(COUNT=COUNT2)
TID = REAL(COUNT2 - COUNT1)/REAL(COUNT_RATE)
WRITE(*,*) ' Beräkningen tar ', TID, ' sekunder'
END PROGRAM TEST_ADAPTIV_KVAD
Vi får naturligtvis inte glömma bort integranden, vilken jag dock låter ligga
i samma fil som huvudprogrammet. Deklarationen är av den nya typen, speciellt vad gäller
att resultatet returneras i en särskild variabel.
FUNCTION F(X) RESULT (FUNKTIONSVAERDE)
IMPLICIT NONE
REAL, INTENT(IN) :: X
REAL :: FUNKTIONSVAERDE
FUNKTIONSVAERDE = EXP(-X**2)
END FUNCTION F
Nu är det dags att provköra på Sun-datorn. Jag har redigerat utmatningen något
för att få den mer koncentrerad. Feluppskattningen är relativt realistisk i
varje fall med denna integrand, den onormaliserade felfunktionen.
Huvudprogrammet och funktionen f(x) finns i filen test_kva.f90, medan den rekursiva funktionen finns i kvad.f90 Dessa kan hämtas med WWW och kan därför enkelt användas för egna tester.
f90 test_kva.f90 kvad.f90
test_kva.f90:
kvad.f90:
a.out
Integralen är 1.7733453512 med feluppskattning 0.0049186843
med verkligt fel 0.0008914471
Integralen är 1.7724548578 med feluppskattning 0.0003375171
med verkligt fel 0.0000009537
Integralen är 1.7724541426 med feluppskattning 0.0000356939
med verkligt fel 0.0000002384
Integralen är 1.7724540234 med feluppskattning 0.0000046571
med verkligt fel 0.0000001192
Integralen är 1.7724539042 med feluppskattning 0.0000004876
med verkligt fel 0.0000000000
Jag har kört programmet på ett antal olika system och fått följande resultat. Vid upprepad körning varierar körtiden något.
| Dator | Tid | Precision |
|---|---|---|
| sekunder | decimala siffror | |
| PC Intel 486 SX 25 | 74,8 | 6 |
| PC Intel 486 DX 50 | 2,75 | 6 |
| PC Intel Pentium 200 | 0,26 | 6 |
| Sun SPARC SLC | 2,50 | 6 |
| Sun SPARC station 10 | 0,58 | 6 |
| Cray Y-MP | 0,19 | 14 |
| Cray C 90 | 0,13 | 14 |
| DEC Alpha 3000/900 | 0,06 | 6 |
| DEC Alpha 3000/900 | 0,06 | 15 |
| DEC Alpha 3000/900 | 3,32 | 33 |
Anm. Ovanstående program är skrivet på ett mycket direkt sätt för att illustrera rekursiv och adaptiv teknik. Det är därför inte optimerat, en enkel optimering föreslås i övning (22.14).
SUBROUTINE SOLVE(F, A, B, TOL, EST, RESULTAT)
REAL, EXTERNAL :: F
REAL, OPTIONAL, INTENT (IN) :: A
REAL, OPTIONAL, INTENT (IN) :: B
REAL, OPTIONAL, INTENT (IN) :: TOL
REAL, INTENT(OUT), OPTIONAL :: EST
REAL, INTENT(OUT) :: RESULTAT
IF (PRESENT(A)) THEN
TEMP_A = A
ELSE
TEMP_A = 0.0
END IF
IF (PRESENT(B)) THEN
TEMP_B = B
ELSE
TEMP_B = 1.0
END IF
IF (PRESENT(TOL)) THEN
TEMP_TOL = TOL
ELSE
TEMP_TOL = 0.001
END IF
! Här skall den verkliga beräkningen finnas, men den
! är här ersatt med enklast tänkbara approximation,
! nämligen mittpunktsapproximation utan feluppskattning.
RESULTAT = (TEMP_B - TEMP_A) &
* F(0.5*(TEMP_A+TEMP_B))
IF (PRESENT(EST)) EST = TEMP_TOL
RETURN
END SUBROUTINE SOLVE
Den förenklade integralberäkningen ovan kan exempelvis ersättas med den adaptiva
kvadraturen i övning (5.5).
INTERFACE
SUBROUTINE SOLVE (F, A, B, TOL, EST, RESULTAT)
REAL, EXTERNAL :: F
REAL, INTENT(IN), OPTIONAL :: A
REAL, INTENT(IN), OPTIONAL :: B
REAL, INTENT(IN), OPTIONAL :: TOL
REAL, INTENT(OUT), OPTIONAL :: EST
REAL, INTENT(OUT) :: RESULTAT
END SUBROUTINE SOLVE
END INTERFACE
(9.1) Variablerna A och B tilldelas angivna
värden, men hela resten av raden blir kommentar!
(9.2) Nej, på den andra raden är det blanka tecknet efter & ej tillåtet. Det bryter nämligen identifieraren ATAN i två. Om det blanka tecknet tas bort blir raderna korrekta. Fri form förutsättes, eftersom & ej är fortsättningstecken i fix form.
INTEGER, PARAMETER :: DP = SELECTED_REAL_KIND(15,99)
(10.2)
REAL (KIND=DP) :: E, PI
(10.3)
REAL (KIND=DP), PARAMETER :: E = 2.718281828459045_DP, &
PI = 3.141592653589793_DP
(12.1) Jag antar att vektorn har en fix dimensionering, samt gör en kontrollutmatning av
ett par värden.
REAL, TARGET, DIMENSION(1:100) :: VEKTOR
REAL, POINTER, DIMENSION(:) :: UDDA, JAEMNA
UDDA => VEKTOR(1:100:2)
JAEMNA => VEKTOR(2:100:2)
JAEMNA = 13 ; UDDA = 17
WRITE(*,*) VEKTOR(11), VEKTOR(64)
END
(12.2) Jag antar att den givna vektorn även här har en fix dimensionering.
REAL, TARGET, DIMENSION(1:10) :: VEKTOR
REAL, POINTER, DIMENSION(:) :: PEKARE1
REAL, POINTER :: PEKARE2
PEKARE1 => VEKTOR
PEKARE2 => VEKTOR(7)
(14.1) Använd funktionerna
MIN och
MAX för att finna
minsta respektive största
värde av alla kombinationer A%LAEGRE * B%LAEGRE, A%LAEGRE * B%OEVRE, A%OEVRE * B%LAEGRE och
A%OEVRE * B%OEVRE vid multiplikation, och motsvarande vid division.
(14.2) Testa om B%LAEGRE <= 0 <= B%OEVRE, i vilket fall felutskrift skall ske.
(14.3) Eftersom vi inte har direkt tillgång till maskinaritmetiken (dvs kommandon av typ avrunda nedåt respektive avrunda uppåt) så kan man få en hyfsad simulering genom att minska respektive öka med avrundningskonstanten. I princip dubbleras då effekten från avrundningen.
(16.1) Om detta misslyckas är det troligen fel redan i det ursprungliga Fortran 77 programmet, eller Du har utnyttjat någon utvidgning från standard Fortran 77.
(16.2) Om detta misslyckas beror det troligen på att felaktiga kommandon tolkades som variabler under fix form, men nu när blanka är signifikanta upptäcks den felaktiga syntaxen.
Notera även att eventuell text i positionerna 73 till 80 under fix form normalt behandlas som kommentar (till exempel radnummer).
(16.3) Fortran 77 ger inget fel varken under kompilering eller exekvering. Kompilering under Fortran 90 fix form ger en varning från kompilatorn att variabeln ZENDIF användes utan att ha tilldelats något värde. Programmet tolkas nämligen så att THENZ, ELSEY och ZENDIF blir vanliga flyttalsvariabler. Kompilering under Fortran 90 fri form ger däremot ett antal syntaxfel. Den rätta versionen av programmet skall nämligen innehålla tre ytterligare vagnreturer, se nedan.
LOGICAL L
L = .FALSE.
IF (L) THEN
Z = 1.0
ELSE
Y = Z
END IF
END
Anmärkning. Även vissa Fortran 77 kompilatorer ger varning om variabeln
ZENDIF.
(22.1) Under fix form betyder den LOGICAL L, dvs variabeln L deklareras som logisk. Under fri form blir det syntaxfel.
REAL,PARAMETER :: K = 0.75
INTEGER, DIMENSION(3,4) :: PELLE
INTEGER, PARAMETER :: DP = SELECTED_REAL_KIND(15,99)
REAL (KIND=DP) :: E, PI
E = 2.718281828459045_DP ; PI = 3.141592653589793_DP
(22.7) Nej, den är inte korrekt eftersom ett kommatecken fattas mellan REAL och DIMENSION. I den form som den skrivits tolkas satsen som en deklaration (gamla typen) av flyttalsmatrisen DIMENSION och en implicit deklaration (nya typen) av ett skalärt flyttal AA. Strikt formellt är det dock en korrekt deklaration. Variabelnamnet DIMENSION är tillåtet under Fortran 90, men det är naturligtvis för långt under Fortran 77.
(22.8) Ja, den är korrekt men den är mindre lämplig eftersom den dödar den inbyggda funktionen REAL för explicit konvertering av en variabel av annan typ till typen REAL. Det är dock inget som hindrar att man har en variabel av typ REAL med namnet REAL, eftersom Fortran inte har reserverade ord.
(22.9) Nej, den är inte korrekt, vid COMMON användes inte dubbelkolon vid deklaration, i princip eftersom COMMON är ett utgående kommando. Den rätta deklarationen är den gamla hederliga
COMMON A
(22.10) Satsen är ej tillåten, vilket dock visar sig först vid exekvering. Man kan i stället skriva
WRITE(*,*) ' HEJ '
eller
WRITE(*,'(A)') ' HEJ '
vilka båda skriver ut texten HEJ på standardenheten
för utmatning. Om man vill ge den text man vill mata ut direkt på
den plats där utmatningsformatet skall ges kan man antingen använda
apostrofeditering
WRITE(*, "(' HEJ ')")
eller den föråldrade Hollerith-räknaren
WRITE(*, "(5H HEJ )")
(22.11) De skriver ut till beloppet stora eller små tal med en heltalssiffra, sex decimaler och exponent, medan tal mittemellan skrivs på ett naturligt sätt. Vi får således i detta fall
1.000000E-03
1.00000
1.000000E+06
Talen från 0,1 till 100 000 skrivs ut på det naturliga sättet, och med sex signifikanta
siffror.
SELECT CASE (N)
CASE(:-1)
! Fall 1
CASE(0)
! Fall 2
CASE(3,5,7,11,13)
! Fall 3
END SELECT
(22.13)
SUMMA = 0.0
DO I = 1, 100
IF ( X(I) == 0.0 ) EXIT
IF ( X(I) < 0.0 ) CYCLE
SUMMA = SUMMA + SQRT(X(I))
END DO
Om man i stället använder en FORALL-konstruktion måste man notera
att i DO-satsen tolkas "aktuellt" värde som det första med angiven egenskap (nämligen noll),
varvid beräkningen skall avbrytas enligt specifikationen av uppgiften. Detta fungerar då inte vid den mer parallella
FORALL-konstruktionen, som är olämplig i detta fall.
Anm. Uppgiften är inte helt entydig, eftersom man kan tänkas utföra DO-satsen i annan ordning!
(22.14) Denna övning består i att optimera det adaptiva programmet för numerisk kvadratur (se Övning (5.5) och dess lösning) genom att minska antalet funktionsanrop av funktionen f(x).
Vi noterar att vid varje anrop av den rekursiva funktionen beräknas funktionsvärdet i de båda ändpunkterna samt i mittpunkten (det senare till och med två gånger)!
Det modifierade huvudprogrammet och funktionen f(x) finns i filen test_kv2.f90, medan den modifierade rekursiva funktionen finns i kvad2.f90 Även dessa kan hämtas med WWW och kan därför enkelt användas för egna tester.
Följande ändringar har gjorts: