Appendix 12. Laborationer

This Appendix with Computer Exercises is also available in English

• A 12.0 Inledning
• A 12.1 Laboration 1 (Runge-Kutta)
• A 12.2 Laboration 2 (Horners schema och filhantering)
• A 12.3 Laboration 3 (Fakultet och Bessel)
• A 12.4 Laboration 4 (Fakultet och Runge-Kutta)
• A 12.5 Laboration 5 (Linjärt ekvationssystem och filhantering)
• A 12.6 Laboration 6 (Fakultet)
• A 12.7 Laboration 7 (Bessel)
• A 12.8 Laboration 8 (Runge-Kutta)
• A 12.9 Laboration 9 (Egna datatyper)
• A 12.10 Laboration 10 (Egen sinus)
• A 12.11 Laboration 11 (Instabil algoritm)
• A 12.12 Laboration 12 (Intervallaritmetik)
• A 12.13 Laboration 13 (Binär stjärna)
• A 12.14 Laboration 14 (Logisk funktion med textsträngs-argument)
• A 12.15 Laboration 15 (Skalär och vektor-produkter)
• A 12.16 Laboration 16 (Ekologisk differentialekvation)

A 12.0 Inledning

Laborationerna sex till åtta är nytillkomna hösten 2001, delvis beroende på datorbytet vid Matematiska Institutionen vid Linköpings Tekniska Högskola. Däremot användes inte längre laboration ett. Laboration nio kom hösten 2002, laborationerna tio och elva hösten 2004 och laborationerna tolv till femton kom hösten 2005.

När jag nedan skriver kursbiblioteket så är det en hänvisning till att respektive filer bör göras tillgängliga på lämpligt sätt för eleverna, men vid exempelvis självstudier kan man själv skriva in dem på ett lämpligt filbibliotek. Alternativt kan man hämta filerna från vårt kursbibliotek. Aktuella filer finns även bland övriga exempel i katalogen kod. Under UNIX är det lätt att införa symboliska namn på bibliotek, så jag kan kalla kursbiblioteket för $KURSBIB i stället för det fullständiga namnet på biblioteket på vårt lokala system, nämligen /mailocal/lab/numt/TANA70/

Lokalt gäller att både Fortran 77, Fortran 90 och Fortran 95 är tillgängliga på MAI:s Sun arbetsstationer.

Ytterligare information om kursen (även tidigare elevers synpunkter) finns på URL = http://www.mai.liu.se/~boein/kurser/TANA70

Lämplig miljö erhålles med kommandona

setenv KURSBIB /mailocal/lab/numt/TANA70/
set path=(/mailoca/lab/numt/TANA70 ./ $path)
module add workshop

source /mailocal/lab/numt/TANA70/.cshrc

TANA70setup

Ytterligare information om DEC Fortran 90, dess system parametrar, tips om kompilering, samt några exempel finns fortfarande tillgängliga.

A 12.1 LABORATION 1

Runge-Kutta

Pascal-programmet nedan för lösning av en ordinär differentialekvation med Runge-Kuttas metod finns på kursbiblioteket, nämligen på filen lab1.p. Din uppgift är att översätta det från Pascal till Fortran. Utskriften från programmet skall förutom siffervärden innehålla lämplig text. Det erfordras ej men betraktas som en fördel om programmet även ändras till att kunna använda andra startvärden på x och y än de i Pascal-programmet inbyggda, nämligen 1 och 2.

Följande skall lämnas in:

• a) Lista på det översatta programmet.
• b) Lista (vid UNIX från script) på körning av de fyra testfallen

        Antal steg      Steglängd

             1               1
             2               0.5
             4               0.25
             8               0.125

Uppgiften är således att med Runge-Kuttas metod lösa differentialekvationen y'(x) = x² + sin(xy) med begynnelsevärdet y(1) = 2 fram till x = 2 med ovan angivna steglängder. Formlerna för Runge-Kuttas metod finns bland annat i beskrivningen av laboration 8.

program RK1;
    (* Enkelt program i Pascal för Runge-Kuttas metod för 
       första ordningens differentialekvation.
                dy/dx = x^2 + sin(xy)
                y(1) = 2                                 *)
var     antal, i : integer;
        h, k1, k2, k3, k4, x, y : real;
        function f(x,y : real) : real;
            begin
                  f := x*x + sin(x*y)
            end;
begin
      antal := 1;
        while antal > 0 do
        begin
            x := 1.0;
            y := 2.0;
            writeln(' Ge antal steg ');
            read(antal);
            if antal >= 1 then
                begin
                        writeln(' Ge steglängd ');
                        read(h);
                        writeln('       x              y');
                        writeln(x, y);
                        for i := 1 to antal do
                        begin
                                k1 := h*f(x,y);
                                k2 := h*f(x+0.5*h,y+0.5*k1);
                                k3 := h*f(x+0.5*h,y+0.5*k2);
                                k4 := h*f(x+h,y+k3);
                                x  := x + h;
                                y  := y + (k1+2*k2+2*k3+k4)/6;
                                writeln(x, y);
                        end;
                end;
        end;
end.

program RK1;

program RK1(INPUT, OUTPUT);

A 12.2 LABORATION 2

Horners schema och filhantering

Programmet finns numera även i Fortran 90 fri form som lab2.f90.

Följande skall lämnas in:

• a) Lista på det rättade och modifierade programmet.
• b) Lista (vid UNIX från script) på körning av de tre testexemplen (x*x + 2 = 0) respektive lab21.dat och lab22.dat.

******************************************************************************
**      Programmet beräknar alla rötter (reella och komplexa) till ett      **
**      N:te-gradspolynom med komplexa koefficienter. (N <= 10)             **
**                                                                          **
**                 n        n-1                                             **
**       P(z) = a z  + a   z    + ... + a z + a                             **
**               n      n-1              1     0                            **
**                                                                          **
**      Avbrott sker om                                                     **
**                 1) Abs (Z1-Z0) < EPS       ==>   Roten funnen = Z1       **
**                 2) ITER > MAX         Långsam konvergens   ==>   Avbrott **
**                                                                          **
**      Programmet sätter EPS till 1.0E-7 och MAX till 30                   **
**                                                                          **
**      Använd metod är NEWTON-RAPHSONS metod:  z1 = z0 - P(z0)/P'(z0)      **
**      Värdet av P(z0) och P'(z0) beräknas med hjälp av HORNERS SCHEMA.    **
**                                                                          **
**      Fältet A(0:10) innehåller polynomets komplexa koefficienter.        **
**      Fältet B(1:10) innehåller de komplexa koefficienterna till          **
**      polynomet Q(z),                                                     **
**                  där P(Z) = (z-z0)*Q(z) + P(z0)                          **
**      Koefficienterna till Q(z) erhålles med hjälp av HORNERS SCHEMA.     **
**                                                                          **
**      När första roten erhållits med NEWTON-RAPHSONS metod, divideras den **
**      bort (s.k. deflation). Kvotpolynomet  = Q(z).                       **
**      Proceduren upprepas därefter med koefficienterna till Q(z) som      **
**      indata.                                                             **
**      Som startapproximation används i samtliga fall STARTV = 1+i         **
**      Z0 är föregående approximation till roten.                          **
**      Z1 är senast beräknade approximation till roten                     **
**      F0 = P(Z0)                                                          **
**      FPRIM0 = P'(Z0)                                                     **
******************************************************************************
      COMPLEX      A(0:10), B(1:10), Z0, Z1, STARTV
      INTEGER      N, I, ITER, MAX
      REAL         EPS
      DATA  EPS/1E-7/, MAX /30/, STARTV /(1,1)/
******************************************************************************
20    WRITE(6,*)  'Ange polynomets gradtal'
      READ (5,*) N
      IF (N .GT. 10) THEN
         WRITE(6,*) 'Polynomets gradtal får inte vara större än 10'
      GOTO 20
      WRITE (6,*) 'Ge polynomets koefficienter, som komplexa konstanter'
      WRITE (6,*) 'Högstagradskoefficienten först'
      DO 30 I = N, 0, -1
          WRITE (6,*) 'A(' , I, ') = '
          READ  (5,*)  A(I)
30    CONTINUE
      WRITE (5,*) '    Rötterna är','            Antal Iterationer'
******************************************************************************
40    IF (N GT 0) THEN
C     ******     Finn nästa rot     ******
          Z0 = (0,0)
          ITER = 0
          Z1 = STARTV
50        IF (ABS(Z1-Z0) .GE. EPS) THEN 
C         ++++++ Fortsätt iterera tills två efterföljande rötter ++++++
C         ++++++ är tillräckligt nära varandra.                  ++++++
              ITER = ITER + 1
              IF (ITER .GT. MAX) THEN
C             ------   För många iterationer  ==> Avbrott  ------
                  WRITE (6,*) 'För många iterationer.'
                  WRITE (6,*) 'Senaste approximationen till roten är ',Z1
              GOTO 200
              ENDIF
              Z0 = Z1
              HORNER (N, A, B, Z0, F0, FPRIM0)
C             ++++++   NEWTON-RAPHSONS METOD                 ++++++
              Z1 = Z0 - F0/FPRIM0
          GOTO 50
          ENDIF
C         +++++++++++++++++++++++++++++++++++++++++++++++++++++++++
100       WRITE (6,*) Z1, '         ',Iter
C         ****** Roten funnen. Dividera bort den och sök nästa rot ******
          N = N - 1
          FOR I = 0 TO N DO
              A(I) = B(I+1)
      GOTO 40
      ENDIF
200   END

      SUBROUTINE  HORNER(N, A, B, Z, F, FPRIM)
******    Parametrarnas betydelse - se huvudprogrammet   ******
******    BI och CI hjälpvariabler.                      ******

      INTEGER N, I
      COMPLEX A(1:10), B(0:10), Z, F, FPRIM, BI, CI

      BI = A(N)
      B(N) = BI
      CI = BI

      DO 60  I = N-1, 1, -1
             BI = A(I) + Z*BI
             CI = BI + Z*CI
             B(I) = BI
C            ++++++ BI = B(I) för beräkning av P(Z) ++++++
C            ++++++ CI  för beräkning av P'(Z)      ++++++
60    CONTINUE

      F = A(0) + Z*BI
      FPRIM = CI

      RETURN
      END
******   SLUT  HORNERS SCHEMA                                ******

******   Programmet är komponerat av Ulla Ouchterlony 1984   ******

1. Läs programmet och rätta de fel Du hittat.

2. Kör programmet och se om det fungerar till belåtenhet.

3. Om det ej fungerar, rätta de fel som Du hittat nu och gå till punkt 2. Om Du inte hittar något fel kompilerar Du om programmet med påslagen kontroll av odeklarerade variabler. Detta sker under vissa system med

                   f77 -u lab2.f
                   a.out
   

   Under moderna system, till exempel Fortran 90, lägger man i stället in satsen IMPLICIT NONE först i både huvudprogram och subrutin. Hos Absoft har -u en helt annan betydelse, jag har inte hittat motsvarande kommando under denna kompilator.

4. Rätta de fel som Du hittat nu och gå till punkt 2. Om Du inte hittar något fel kompilerar Du nu om programmet med påslagen kontroll av fältindex. På vissa system kan detta ske med följande kommandon.

                   f77 -C lab2.f
                   a.out
   

   Under Absoft ger man istället f90 -Rb och vid Intel ifort ger man ifort -CB.

5. Rätta de fel som Du hittat nu och gå till punkt 2.

6. Om Du inte hittar felet, det blir till exempel fel resultat eller utskriften "segmentation error", så kan Du försöka med avlusaren eller debuggern. På de flesta UNIX-system startar Du denna med kommandot

         dbx a.out
   

   om Ditt kompilerade program heter a.out. Som första kommando ger Du run och kör sedan som vanligt. Eventuella fel under exekveringen kommer nästan ut i klartext! För att komma ut från debuggern skriver Du quit. Se även kapitel 17.

7. När programmet fungerar börjar Du med att modifiera programmet till att kunna hantera indata även från fil.

8. Hur man öppnar en fil framgår av avsnittet 8.1.

9. Vid liststyrd inmatning av text bör texten inneslutas inom apostrofer (kräves på vissa system). Detta är obekvämt för användaren. Man bör därför i stället använda formatstyrd inmatning. Om man skall mata in ett tecken användes lämpligen FORMAT(A1), om det gäller 13 tecken användes lämpligen FORMAT(A13).

10. Kom ihåg att en läs- eller skrivsats i en explicit DO-slinga alltid börjar med en ny post (ny rad). Om man har flera data på samma rad måste dessa därför läsas med samma lässats, varvid man kan använda en implicit DO-slinga, se avsnitt 7.5.

    Den explicita DO-slingan nedan kommer att skriva sju rader, var och en med ett värde av X

    	DO I = 1, 13, 2
    	   WRITE(*,*) X(I)
    	END DO
    

    Den implicita DO-slingan nedan kommer att skriva en rad med sju värden av X

     	WRITE(*,*) ( X(I), I = 1, 13, 2)
    

11. Kom ihåg att eftersom Newton-Raphson bara är garanterat konvergent nära roten finns det ingen garanti för att det rättade programmet fungerar på godtyckliga indata.

12. Enligt standarden skall komplexa tal skrivas med parentes om realdel och imaginärdel, även om imaginärdelen är noll, som i (1.0, 0.0). Vissa kompilator, bland annat Intel ifort tillåter att man i detta fall bara skriver realdelen enligt 1.0, varvid imaginärdelen automatiskt blir noll.

    Prova gärna om ditt system tillåter detta förenklade skrivsätt, men använd det då bara vid inmatning via tangentbordet och aldrig vid inmatning från fil (av portabilitetsskäl).

A 12.3 LABORATION 3

Fakultet och Bessel

Deluppgift a)

Deluppgift b)

Vid användning av NAG:s Fortran 77 bibliotek har man nytta av NAG User Notes, vilka beskriver de maskinspecifika delarna.

Aktuell Bessel-funktion i NAG-biblioteket heter S17AEF och har argumenten X och IFAIL och i denna ordning, där X är argumentet för Bessel-funktionen i enkel eller dubbel precision, och där IFAIL är en felparameter (heltal). Denna senare sättes lämpligen till 1 vid ingången och avläses vid återhoppet. Om den då är noll så är allt OK, om den är 1 så är argumentet för stort (till beloppet).

Om NAG-biblioteket är installerat på normalt vis länkar man in det med kommandot

        f77 prog.f -lnag

Det är även tillåtet att använda NAG:s nya Fortran 90 bibliotek. Notera att funktionerna har andra namn i detta bibliotek (vår Bessel-funktion heter nag_bessel_j0). Du måste använda en eller flera moduler, till exempel

        USE nag_bessel_fun, ONLY : nag_bessel_j0

        f90 prog.f90 -lnagfl90

Om Du däremot använder Fortran 90 men Du fortfarande har NAG-biblioteket i Fortran 77 måste metod 2 från kapitel 15 användas, dvs man kompilerar och länkar in erforderliga bibliotek med ett implementationsberoende kommando, till exempel på Sun

        f90 prog.f -lnag -lF77

        f90 prog.f -lnag -lfor -lutil -li -lots

På DEC UNIX är -lfor -lutil -lots tillgängliga, men inget av dem behövs.

Observera i vilken precision NAG-biblioteket finns på just Din maskin! Gör Du fel med precisionen blir resultatet oftast fullständigt galet.

Lokalt gäller att NAG-biblioteket ej finns på Sun-systemet vid MAI.

Deluppgift c)

Skriv ett program för tabellering av Bosses funktionen Bo(x). Använd därvid biblioteket libbosse.a på kursbiblioteket. Skriv gärna huvudprogrammet så att det ber om det intervall för vilket funktionen önskas beräknad. Mata ut en tabell med x och Bo(x) för x = 0.0, 0.1, ... 1.0. Se till att utmatningen ser snygg ut! Provkör! Undersök även vad som händer vid argumenten + 800 och -900!

Aktuell Bosse-funktion heter BO och har argumenten X och IFAIL och i denna ordning, där X är argumentet för Bosse-funktionen i enkel eller dubbel precision, och där IFAIL är en felparameter (heltal). Denna senare sättes lämpligen till 1 vid ingången och avläses vid återhoppet. Om den då är noll så är allt OK, om den är 1 så är argumentet för stort, om den är 2 så är argumentet för litet. Denna felhantering är samma som hos NAG, om IFAIL är 0 vid ingången kommer programmet vid ett fel att stanna med en felutskrift från felhanteringsfunktionen, och aldrig komma tillbaks till Ditt program!

Om Bosses bibliotek är installerat på normalt vis länkar man in det med kommandot

        f77 prog.f -L$KURSBIB -lbosse 

Om Du däremot använder Fortran 90 men Du fortfarande har Bosses bibliotek i Fortran 77 måste metod 2 från kapitel 15 användas, dvs man kompilerar och länkar in erforderliga bibliotek med ett implementationsberoende kommando, se ovan i deluppgift b). För att göra livet lättare har jag dock gjort även en Fortran 90 version av mitt bibliotek, vilket användes utnyttjande

        f90 prog.f90 -L$KURSBIB -lbosse90 

        f90 prog.f90 -lbosse90 -L$KURSBIB

Anmärkning 2. Observera i vilken precision Bosses bibliotek finns på just Din maskin! Gör Du fel med precisionen blir resultatet oftast fullständigt galet.

Lokalt gäller att Bosses bibliotek är i dubbel precision på Sun-systemet.

A 12.4 LABORATION 4

Fakultet och Runge-Kutta

Deluppgift a)

Deluppgift b)

        y'(t) = z                           y(0) = 1
        z'(t) = 2*y*(1+y^2) + t*sin(z)      z(0) = 2

Notera att det av mig införda förbudet att i just denna laboration använda externa funktioner försvårar användning av underprogram för utförande av Runge-Kutta stegen. Enda syftet med detta förbud är att tvinga till övning i lokala funktioner.

Formlerna för Runge-Kutta vid system finns här!

A 12.5 LABORATION 5

Linjärt ekvationssystem och filhantering

Kommentarer:

• Det är meningen att huvudprogrammet skall ha en meny (gärna utnyttjande SELECT CASE) där man väljer vilket av nedanstående underprogram som skall utföras. När ett underprogram har exekverats kommer man tillbaks till menyn för ett nytt val.

• Huvudprogrammet utnyttjar LASMAT, LASVEK, MATIN och VEKIN för att få in matrisen A och vektorn b, anropar lösningsprogrammet LOS och skriver ut matris A, högerled b och lösning x med hjälp av MATUT och VEKUT.

• Programmet skall kontrollera att man exempelvis inte försöker skriva ut en lösning med VEKUT förrän en sådan har beräknats med LOS.

• Om dimensionen på matrisen och vektorn ej överensstämmer skall programmet (underprogrammet eller huvudprogrammet) ge en felutskrift, liksom om den givna rutinen upptäcker singularitet för matrisen eller något annat problem.

• Dimensioneringen skall utnyttja de dynamiska möjligheterna i Fortran 90/95. En lämplig metod kan vara att utnyttja pekare vid deklarationen, se avsnitt 4.3.2, eller (vilket är att föredraga) att utnyttja en modul, se slutet av nämnda avsnitt eller exemplet.

• Programmet skall efter avslutad beräkning och utmatning gå tillbaks till startpunkten och begära ny matris och/eller nytt högerled. Det skall vidare vara möjligt att utnyttja huvudprogrammet för att (utan förnyad manuell inmatning) utnyttja redan på filer undanlagrade matriser och vektorer. I uppgiften ingår bland annat att göra ytterligare nödvändiga specifikationer, testa rimligheten av inlästa värden, samt att hitta på de testmatriser och testvektorer som skall utnyttjas för att testa programmet.

Det första underprogrammet LASMAT skall interaktivt läsa in flyttalsvärdena i en kvadratisk matris. Programmet skall fråga efter dimension samt ge användaren möjlighet att individuellt mata in enbart de värden som är skilda från noll. Därefter skall programmet lagra undan den fulla matrisen (den eventuella glesa egenskapen får inte utnyttjas vid lagringen) på en fil utnyttjande maximal noggrannhet och minimalt lagringsutrymme. Underprogrammet skall fråga användaren efter namnet på filen, men filtypen skall vara .mat. Användaren får ej ge filtypen.

Kommentarer till LASMAT:

• Det är lämpligt att använda två olika sätt att läsa in matrisen, nämligen dels en metod som läser in matrisen rad för rad, dels en som läser in rad, kolumn och värde för de nollskillda elementen. Den första metoden är bra för att läsa in de båda testmatriserna!

• Kravet med "maximal noggrannhet och minimalt lagringsutrymme" innebär att man skall använda oformatterad utmatning, jämför med inledningen till kapitel 7 om in- och utmatning samt sektion 19.3 .

Det andra underprogrammet LASVEK skall interaktivt läsa in flyttalsvärdena i en vektor. Programmet skall fråga efter dimension samt ge användaren möjlighet att individuellt mata in enbart de värden som är skilda från noll. Därefter skall programmet lagra undan den fulla vektorn (den eventuella glesa egenskapen får inte utnyttjas vid lagringen) på en fil utnyttjande maximal noggrannhet och minimalt lagringsutrymme. Underprogrammet skall fråga användaren efter namnet på filen, men filtypen skall vara .vek. Användaren får ej ge filtypen.

Det tredje underprogrammet MATIN läser en matris från filen med angivet namn och lagrar den så att den är tillgänglig i det anropande programmet. Användaren får ej ge filtypen.

Det fjärde underprogrammet VEKIN läser en vektor från filen med angivet namn och lagrar den så att den är tillgänglig i det anropande programmet. Användaren får ej ge filtypen.

Det femte underprogrammet MATUT skriver ut en matris på papper (via en fil), med rader och kolumner på normalt sätt om dimensionen är högst 10, och på ett begripligt sätt annars. Radskrivarens 132 positioner i bredd skall utnyttjas väl. Notera att godtyckliga flyttal skall kunna skrivas ut. Utskrift på papper sker normalt via en fil, som sedan skrives ut med ett lpr under UNIX eller motsvarande kommando under Windows.

Det sjätte underprogrammet VEKUT skriver ut en vektor på papper (via en fil), helst dock i transponerad (radvis) form. Notera att det finns både högerled och lösning att skriva ut! Man behöver därför komplettera denna rutin med information om vilken vektor som skrives ut.

Det sjunde underprogrammet LOS löser ekvationssystemet genom att anropa den givna rutinen LOES_LIN_EKV_SYSTEM, som är i dubbel precision. Denna rutin får ej ändras och får ej heller läggas in i en modul.

Ett obligatoriskt testexempel är följande (med en 3 x 3 matris)

		 33	 16	 72			-359
	A =	-24	-10	-57		b =	 281
		 -8	 -4	-17			  85

Ett annat obligatoriskt testexempel är följande (med en 4 x 4 matris)

                  2    3    0    0                        1
                  0    0   1,8  10,1                     11
	A =                                     b =	 
                 0,2  4,3   5    0                       42
                  0   0,8   7    7                      109

Inlämning skall ske av fullständig programlistning, körexempel med gles matris, resultatutskrift av matris med dimensionerna 3, 4, 10 och 12.

• Tips 1. Testa även på det triviala fallet med dimensionen 1 på både matris och vektor.

• Tips 2. Den givna rutinen får ej ändras. Anropet måste därför utnyttja ett så kallat gränssnitt, INTERFACE.

• Tips 3. Utför gärna den första kompileringen av programmet på en programenhet i taget, för att inte bli översvämmad med felutskrifter. När alla programenheterna kan kompileras var för sig kan man förfara på fyra sätt. Jag antar att huvudprogrammet finns på filen huvud.f90, subrutinen LASMAT på filen lasmat.f90, osv, samt ett eventuellt fullständigt program på filen labb5.f90.
  1. Kompilera alla rutinerna var för sig men samtidigt och med samma kommando,

               f90 huvud.f90 lasmat.f90 lasvek.f90 ... loes.f90
     

     Exekvera med

               a.out
     

  2. Kompilera alla rutinerna var för sig helt separat och utnyttja objektmodulerna vid länkning

               f90 -c huvud.f90 
               f90 -c lasmat.f90 
               f90 -c lasvek.f90 
               ...
               f90 -c loes.f90 
               f90 huvud.o lasmat.o lasvek.o ... loes.o
     

     Exekvera med

               a.out
     

     Vid ändring av en rutin behöver bara den kompileras om, varvid länkning av samtliga följer. Denna metod går mycket fortare!

  3. Kombinera alla filerna till en stor fil och kompilera,

                f90 labb5.f90
     

     Exekvera med

                a.out
     

     Denna metod går mycket långsamt!

  4. Kompilera alla rutinerna var för sig men utnyttjande kommandot make. Exekvera med labb5. Detta är en överkurs i UNIX! En lämplig makefile finns nedan och på kursbiblioteket. Detta är den bästa metoden!

labb5:  huvud.o lasmat.o lasvek.o matin.o vekin.o \
                matut.o vekut.o los.o loes.o
        f90 -o labb5 huvud.o lasmat.o lasvek.o matin.o vekin.o \
                matut.o vekut.o los.o loes.o
huvud.o: huvud.f90
        f90 -c huvud.f90
lasmat.o: lasmat.f90
        f90 -c lasmat.f90
lasvek.o: lasvek.f90
        f90 -c lasvek.f90
matin.o: matin.f90
        f90 -c matin.f90
vekin.o: vekin.f90
        f90 -c vekin.f90
matut.o: matut.f90
        f90 -c matut.f90
vekut.o: vekut.f90
        f90 -c vekut.f90
los.o:  los.f90
        f90 -c los.f90
loes.o: loes.f90
        f90 -c loes.f90

I princip fungerar make så att om det som står efter kolon har en senare tidsmarkering än det som står före, så utföres den påföljande raden. Det finns en bok som beskriver make.

Anm. Bakåtstrecket \ markerar fortsättningsrad i UNIX.

Den rutin LOES_LIN_EKV_SYSTEM som skall användas i dubbel precision ligger på kursbiblioteket i enkel precision under namnet loes1.f90, och i dubbel precision under namnet loes.f90 och ser ut som följer.

SUBROUTINE LOES_LIN_EKV_SYSTEM(A, X, B, FEL)
        IMPLICIT NONE
        ! Fältdeklarationer
        DOUBLE PRECISION, DIMENSION (:, :), INTENT (IN)  :: A
        DOUBLE PRECISION, DIMENSION (:),    INTENT (OUT) :: X
        DOUBLE PRECISION, DIMENSION (:),    INTENT (IN)  :: B
        LOGICAL, INTENT (OUT)                            :: FEL

        ! Arbetsarean M är A utvidgad med B
        DOUBLE PRECISION, DIMENSION (SIZE (B), SIZE (B) + 1) :: M
        INTEGER, DIMENSION (1)                               :: MAX_LOC
        DOUBLE PRECISION, DIMENSION (SIZE (B) + 1)           :: TEMP_ROW 
        INTEGER                                              :: N, K
  
        ! Initiera M
        N = SIZE (B)
        M (1:N, 1:N) = A
        M (1:N, N+1) = B

        ! Triangulariseringsfas
        FEL = .FALSE.
        TRIANG_SLINGA: DO K = 1, N - 1
                ! Pivotering
                MAX_LOC = MAXLOC (ABS (M (K:N, K)))
                IF ( MAX_LOC(1) /= 1 ) THEN
                    TEMP_ROW (K:N+1 ) = M (K, K:N+1)
                    M (K, K:N+1) = M (K-1+MAX_LOC(1), K:N+1)
                    M (K-1+MAX_LOC(1), K:N+1) = TEMP_ROW (K:N+1)
                END IF

                IF (M (K, K) == 0.0D0) THEN
                        FEL  = .TRUE.     ! Singulär matris A
                        EXIT TRIANG_SLINGA
                ELSE
                        TEMP_ROW (K+1:N) = M (K+1:N, K) / M (K, K)
                        M (K+1:N, K+1:N+1) = M (K+1:N, K+1:N+1)  &
                           - SPREAD( TEMP_ROW (K+1:N), 2, N-K+1) &
                           * SPREAD( M (K, K+1:N+1), 1, N-K)
                        M (K+1:N, K) = 0 ! Dessa värden används ej
                END IF
        END DO TRIANG_SLINGA

        IF (M (N, N) == 0.0D0) FEL  = .TRUE.  ! Singulär matris A

        ! Återsubstitution
        IF (FEL) THEN
           X = 0.0D0
        ELSE
           X (N) = M (N, N+1)/ M (N, N)
           DO K = N-1, 1, -1
              X (K) = M (K, N+1) - SUM (M (K, K+1:N) * X (K+1:N))
              X (K) = X (K) / M (K, K)
           END DO
        END IF

END SUBROUTINE LOES_LIN_EKV_SYSTEM

Anm: Rutinen ovan utnyttjade i en tidigare version summation av tomma vektorer, dvs i princip SUM(vektor(N+1:N)), där vektorn är dimensionerad att ha högst N element, dvs vi har indexöverskridande. Regeln för summationsrutinen SUM är att i sådant fall (på grund av att summation baklänges är begärd) att summera inget element, och således få värdet noll. Jämför med DO-slingan baklänges. Om man kompilerar med indexkontroll, till exempel med f90 -C loes.f90 erhålles naturligtvis felutskrift om otillåtet index vid exekvering. Indexkontroll kan därför ej användas framgångsrikt av den tidigare versionen:

        IF (FEL) THEN
           X = 0.0D0
        ELSE
           DO K = N, 1, -1
              X (K) = M (K, N+1) - SUM (M (K, K+1:N) * X (K+1:N)) 
!             Ovanstående summation är tom om K = N
              X (K) = X (K) / M (K, K)
           END DO
        END IF

Laboration 5, Deluppgift a)

Laboration 5, Deluppgift b)

Laboration 5, Deluppgift c)

Man länkar normalt med

        f90 prog.f90 -lnag

När NAG-biblioteket är kompilerat med Fortran 77, måste ibland metod 2 från kapitel 15 användas, dvs man kompilerar och länkar in erforderliga bibliotek med ett implementationsberoende kommando. Försök dock gärna först utan några extra bibliotek.

Vid deklarationen av fältet för matrisen är det i detta fall valfritt att utnyttja någon av metoderna i a) och b) ovan, dvs utnyttjande antingen en pekare eller en modul med allokerat och sparat fält, eller eventuellt att hitta en egen fungerande metod.

Vid eventuell användning av makefile måste denna naturligtvis justeras.

Laboration 5, Deluppgift d)

Man länkar normalt med

        f90 prog.f90 -lnagfl90

Vid deklarationen av fältet för matrisen är det i detta fall valfritt att utnyttja någon av metoderna i a) och b) ovan, dvs utnyttjande antingen en pekare eller en modul med allokerat och sparat fält, eller eventuellt att hitta en egen fungerande metod.

Vid eventuell användning av makefile måste denna naturligtvis justeras.

Laboration 5, Deluppgift e)

A 12.6 LABORATION 6

Fakultet

Skriv en funktion i Fortran med tillhörande huvudprogram för beräkning av fakulteten. Skriv gärna huvudprogrammet så att det ber om värden på de heltal för vilket fakulteten önskas beräknad. Provkör med olika heltal som indata.

1. Använd genomgående heltal i funktionen. Notera vilket som är det största heltal som fungerar!
2. Använd nu flyttal REAL i funktionen, inargumentet skall dock behållas som heltal. Notera vilket som är det största heltal som fungerar! Det finns nu två svar, dels det största tal som ger helt rätt resultat, dels det största som ger approximativt rätt svar. Man kan även behöva skilja på exakt rätt svar i binär form eller i decimal form!
3. Upprepa med flyttal i dubbel precision. DOUBLE PRECISION i funktionen.
4. Upprepa med flyttal i fyrdubbel precision, om du har tillgång till detta.

A 12.7 LABORATION 7

Bessel-funktionen

Besselfunktioner är lösningar till Bessels differentialekvation

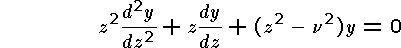
som har fått sitt namn efter Friedrich Wilhelm Bessel (1784 - 1846), som var den förste att studera lösningarna till dem som ett led i hans forskning inom celest mekanik. Konstanten v anger det man kallar ordningen hos ekvationen. Man kan visa att i fallet v = 0 utgör potensserien

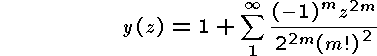
en av de linjärt oberoende lösningarna, den betecknas J₀(z).

Potensserien är konvergent i hela det komplexa talplanet, men på grund av att kancellation kan uppträda nöjer vi oss med beräkning på skivan | z | <= 1.

Uppgiften är nu att i Fortran skriva en funktion i enkel precision som beräknar J₀(z) för sådana argument, och som ser till att varna användaren om argumentet blir för stort (till beloppet), men utan att använda extra in- eller utargument.

Vidare skall funktionen skrivas så att den är generisk, det vill säga en version för komplexa argument och en för reella argument, aktuell version väljes automatiskt. Lämpligt avbrottsvillkor vid summationen är då den tillkommande termen inte ger något ytterligare bidrag till summan. Funktionen skall läggas i en modul, som användes av nedan nämnda huvudprogram.

Skriv ett huvudprogram som använder funktionen för att generera en tabell över J₀(z) på de tre linjerna Re(z) = -0,5; Re(z) = +0,5 och Im(z) = 0 med en lämplig stegning.

Program och körningsresultat skall redovisas.

Laboration 7 b innebär att komplettera programmet till att inte bara klara enkel precision, utan även dubbel och fyrdubbel. Programmet skall bestå av modul(er) och ett huvudprogram, inga andra programenheter.

A 12.8 LABORATION 8

Runge-Kutta

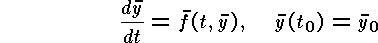
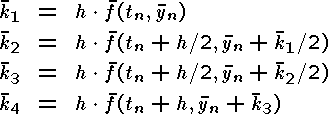
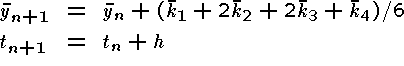
Uppgiften är att skriva en subrutin med inparametrarna t_n, y_n, h och f samt utparametrarna t_n+1 och y_n+1. Här är y en vektor och f(t,y) en vektorvärd funktion av det skalära argumentet t och vektorn y.

Tillämpa ditt program på två valfria av nedanstående tre problem! Beräkna approximationer till y(0.2) genom att använda steglängderna h = 0,04; 0,02 och 0,01. Gör gärna dessutom en manuell Richardson-extrapolation.

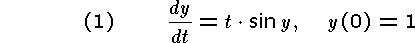
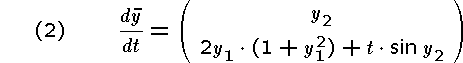
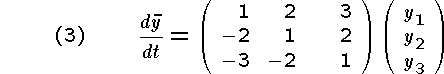
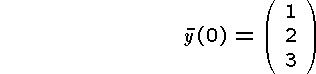
Program och körningsresultat skall redovisas.

Kommentarer:

• Det är naturligt att programmet kommer att bestå av ett huvudprogram, tre funktioner (för de tre högerleden i differentialekvationen) samt en subrutin (för Runge-Kutta beräkningen). Jag rekommenderar att de tre funktionerna läggs i en modul, och subrutinen i en annan modul.

• I subrutinen för Runge-Kutta behövs ett formellt argument för funktionen, som vi kan kalla F(T,Y). Problemet här är att dimensionen på Y kan vara ett, två eller tre! Man behöver där ett INTERFACE som kan se ut ungefär så här

               INTERFACE
  	     FUNCTION F(T,Y) RESULT (FUT)
  	         REAL                     :: T
  		 REAL, DIMENSION(:)       :: Y
  		 REAL, DIMENSION(SIZE(Y)) :: FUT
               END FUNCTION F
               END INTERFACE
  

  Programmet kommer då att vid exekveringen känna av den aktuella dimensionen av Y och tilldela samma dimension till funktionen F (och variabeln FUT). De tre funktionerna måste skrivas på motsvarande sätt, även den första funktionens Y måste skrivas som en vektor (med verklig längd 1) och inte som en skalär.

• Om man inte använder sig av moduler behövs två INTERFACE till!

A 12.9 LABORATION 9

Egna datatyper

Del 1.

Mitt namn är Bo G. Einarsson. Jag är en 65 år gammal manlig
politiker, och jag bor på Ekholmsvägen 249 i Linköping.

Del 2.

Anmärkning:

Egendefinierade datatyper diskuteras i bokens avsnitt 10.5, 12.2, 14.4.2 och A 3.12.

Du får använda en statisk största längd på alla textsträngar. Textsträngar med variabel längd är ett speciellt tillägg till Fortran, se referensen i avsnitt 6.5. Vid utmatning får däremot inte onödigt många blanka skrivas ut. Funktionen LEN_TRIM ger längden av en textsträng utan eventuell(a) avslutande blank(a).

Du får vidare antaga att tilltalsnamnet är första förnamnet och att det bara finns ett extra förnamn vars initial skall med.

Program och körningsresultat skall redovisas.

A 12.10 LABORATION 10

Egen sinus

Om det andra argumentet saknas skall en lämplig noggrannhet väljas!

Skriv ett testprogram och jämför med den inbyggda SIN(X). Precisionen skall kunna vara enkel, dubbel, eller fyrdubbel.

Utvidga programmet till att klara godtyckliga reella värden på X, men i detta fall utan samma krav på noggrannheten.

A 12.11 LABORATION 11

Instabil algoritm

   In = Integral från 0 till 1 av x^n exp(-x) dx

   I0 = 1 - 1/e

   In = -1/e + n In-1      (n = 1, 2, 3, ...)

Betrakta resultatet och jämför med enkla analytiska uppskattningar!

Det finns ett tricks för att beräkna dessa integraler korrekt! Minns du det? Om man startar med ett begynnelsevärde med sex signifikanta siffror kan vi få ett nonsensresultat. Om vi däremot startar med ett värde med inga signifikanta siffror kan vi få sex signifikanta siffror i resultatet! Skriv även detta program!

A 12.12 LABORATION 12

Intervallaritmetik

Din uppgift är att modifiera detta program till att bestämma samtliga nollställen till funktionen

f(x) = exp(-10x²) + cos(pi*x)

i intervallet [-10; 10]. Använd därefter den metodoberoende feluppskattningen till att verifiera de två till beloppet minsta rötterna.

Kompilering sker med kommandot

f95 -xia fil.f90

Jag rekommendar att noggrannhetsparametrarna f_eps och root_eps sänks från nuvarande 10^-5 till högst 10^-10.

A 12.13 LABORATION 13

Binär stjärna

 3,355 - ln(1,352 + cos(pi(t-0,9)/0,7))

 3,598 - ln(1,998 + cos(pi(t-4,4)/0,4))

Skriv en funktion som har tiden t som indata och ljusstyrkan (magnituden) vid denna tidpunkt som utdata. Skriv ett huvudprogram som plottar ljusstyrkan som en funktion av tiden för intervallet t = 0 till t = 25 dagar.

Om du saknar tillgång till plottning i Fortran kan du i stället använda ett annat paket för detta, till exempel MATLAB eller gnuplot. Lite information om hur man utnyttjar MATLAB för plottning finns i slutet av beskrivningen av labb 16.

Anm. Exemplet kan förefalla löjligt, men strålningen från stjärnan Algol (sic!) har faktiskt ett liknande utseende, periodisk med 68 h 50 min, se figur 40 i boken "Big Bang" av Simon Singh! Engelsk pocket ISBN 0-00-715252-3. Svensk inbunden ISBN 91-7343020-X.

A 12.14 LABORATION 14

Logisk funktion med textsträngs-argument

   WITHIN("Jag testar", "test")

   WITHIN("Jag testar", "Test")

Använd gärna en eller flera av de inbyggda ("intrinsic") funktionerna!

Testa din funktion med ett huvudprogram som har inmatning av textsträngar från tangentbordet och använder resultatet av funtionen för att ge en av följande utskrifter

   Frasen 'test' finns i "Jag testar"

   Frasen 'Test' finns inte i "Jag testar"

A 12.15 LABORATION 15

Skalär och vektor-produkter

Använd dessa för att skriva en tredje generisk funktion som beräknar den skalära trippel-produkten, definierad som

    [abc] = a . (b x c)
  

Skriv sedan ett huvudprogram som läser in de tre vektorerna a, b och c och som skriver ut skalärprodukten a . b och vektorprodukten b x c samt den skalära trippelprodukten [abc].

Testa på följande vektorer:

    a = (  1 10  20 )T

    b = (  5  8   9 )T

    c = ( 12 36 108 )T
  

    a = (  1 sqrt(2)  sqrt(3) )T

    b = (  5    8       9  )T

    c = (  2    3       8 )T
  

Anm. Vektorprodukten definieras av

    c = a x b

    c1 = a2 b3 - a3 b2 
    c2 = a3 b1 - a1 b3 
    c3 = a1 b2 - a2 b1
  

A 12.16 Laboration 16

Ekologisk differentialekvation

    u'(t) =  u(t)·[A - 0.1·v(t)]  + 0.015·t,     u(0) = alfa

    v'(t) =  v(t)·[0.02·u(t) - 1] + 0.0075·t,    v(0) = beta 

  

Samtliga storheter är normaliserade, varför den verkliga tidsskalan är okänd, vi kan dock kalla tidsenheten för år. Vi betecknar antalet harar med u(t) och antalet rävar med v(t). Tänk Dig gärna antalen som tusental!

Lösning av detta system av differentialekvationer skall programmeras i Fortran, utnyttjande Runge-Kuttas metod och dubbel precision. Förutom beräkning av antalet harar och rävar skall programmet beräkna det fel i respektive antal som beror på att parametern A inte är exakt 1 utan i stället 1 + dellta. Själva beräkningen skall ske med A = 1 och dellta = 0.02. Aktuell formel blir analog till den i svaret till 10.15 b, dvs (kolla den gärna):

    DELTAun+1 = [1 + h·(1 - 0.1·vn)]·DELTAun - 0.1·h·un·DELTAvn + h·un·dellta

    DELTAvn+1 = [1 + h·(0.02·un - 1)]·DELTAvn + 0.02·h·vn·DELTAun

    DELTAu0 = 0		
    DELTAv0 = 0
    dellta = 0.02

  

Den avser egentligen Eulers metod, men Du får använda den här vid felberäkningen, för att minska programmeringsarbetet.

Anmärkning: Att jag kallat felet ovan för dellta beror på att delta är ett reserverat namn vid fixpunktsaritmetik i Ada.

Din uppgift är att köra programmet med två val av startvärdena alfa (antalet tusental harar vid starttidpunkten) och beta (antalet tusental rävar vid starttidpunkten). Dessa skall båda väljas mellan 20 och 30.

Gör två körningar, och välj ett lämpligt värde på steglängden h. Du skall i båda fallen gå från t = 0 till t = 50.

För varje fall skall Du plotta vardera u ± DELTAu och v ± DELTAv som funktion av t. Dessutom skall Du separat plotta v som funktion av u. Den senare plotten kallas fasplanet.

Plottningen kan ske antingen direkt i Fortran (kräver i så fall tillgång till plottrutiner), eller genom att Fortran-programmet genererar en fil som kan utnyttjas av Matlab (eller gnuplot) för plottning. Man kommer åt till exempel den andra kolumnen av en matris y genom att skriva y(:,2). En möjlighet är att skriva ut t, u, v, DELTAu och DELTAv som fem separata vektorer, som klistras (målas) in i Matlab efter till exempel x = [, avsluta med ]. Alternativt kan man i Fortran skapa en fil med namnet filnamn.m som innehåller erforderlig matris eller vektorer och som kan hämtas in i Matlab med kommandot filnamn där. Som vanligt är det lämpligt att undvika filnamn som användes för olika funktioner i Matlab!

Kommandot load filnamn.mat arbetar däremot normalt med binära filer som har filändelsen .mat och passar bäst ihop med filer skapade i Matlab med kommandot save filnamn.mat. Kommandot load filnamn.txt fungerar däremot utmärkt i vårt fall.

Fall 1.

     alfa =                          beta =

Fall 2.

     alfa =                          beta =

Fall 3.

Fall 4.