Are bigger servers better for high-performance computing? It is often assumed that communication between processors within a compute node must be faster than using Infiniband networking in a cluster. Consequently, I come across scientists asking for big shared memory servers, believing that their simulations would run much faster there. In reality, it is not always so. In the previous post, I wrote about how the VASP application is bottlenecked by memory bandwidth. In such cases, compute work and communication will compete with each other for precious resources, with severe performance degradation as a result.
Consider this experiment. Let us first run a VASP compute job with 512 bands on a single compute node using 1 to 16 cores. This will give us a scaling graph showing what kind of improvement you can get by using more cores in a server. Now, for comparison, we run the same job but with only one core per compute node. This means that the 16-core job uses 16 compute nodes and only communicates over Infiniband. Which scenario will be faster?
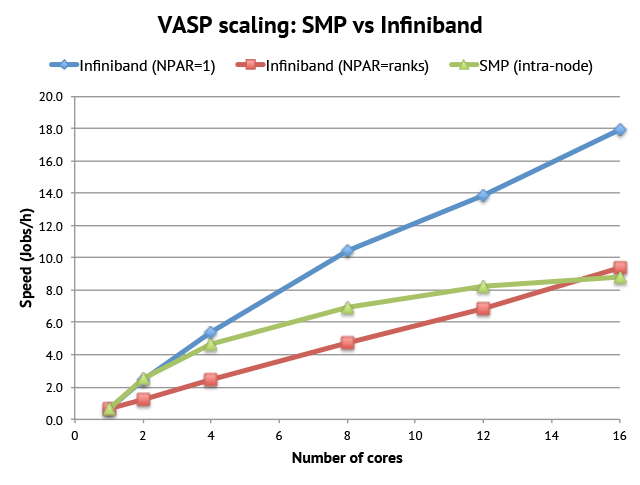
It turns out that communicating only over Infiniband is superior to shared memory. With 16 cores it gives twice as fast calculations. The reason is simply that we throw more hardware at the problem: our processors can now use all the memory bandwidth for computations, while exchanging data over the Infiniband network instead.
The graph above shows that there is no inherent benefit to run an MPI parallelized application such as VASP on a big server vs smaller servers in a cluster connected by Infiniband. The only advantage you get is the increased total amount of available memory per server.
As a user, you can apply techniques like this to speed up your calculations. For example, by using twice as many nodes, but with half the number of cores on each node. On Triolith, you can do like this:
#SBATCH -N 16
#SBATCH --ntasks-per-node 8
mpprun /software/apps/vasp/5.3.3-18Dec12/default/vasp
This will run your application with 8 cores per compute node, for a total of 128 cores. The improvement in speed compared to using 8 full nodes can be as much as 50%, and you will also have twice as much memory available per processor. The drawback is, of course, that you spend twice the core hours on your calculation. But if it is important to get the results quickly, it might be worth it.

