Parallelisation Support of a Large Eddy Simulation Code

NSC have started the code parallelization support of prominent Swedish domain scientists. Scientists can expect the increase of their problem sizes and the reduction of simulation time by this service. This high-end collaboration between NSC and domain scientists will strengthen international competitiveness of top-ranked Swedish scientists and increase NSC’s contribution to Swedish academia.

Prof. Lars Davidson’s LES (Large Eddy Simulation) fluid dynamics code has been chosen as a pilot project of this code parallelization service. This code solves the incompressible Navier-Stokes equations by solving decoupled velocity field (convection-diffusion equation) and pressure field (pressure Poisson equation) iteratively. The convection-diffusion solver uses the conventional 3-dimentional structured stencil, while the pressure Poisson solver applies the multi-grid method and stores the multi-level data on a 1-dimensional array. Minor changes are made on the baseline code for the generic boundary condition imposition, effective memory allocation, and the wall-distance function for the turbulence computation. Mesh partitioner and communicators are implemented for the parallel execution. A structured multi-block partitioner provides the load balanced decomposition at the sufficient multi-grid levels. Communication functions for structured 3-dimensional domains and 1-dimensional multi-grid implementation are incorporated. These implementations are made generic for the direct application to any mesh-based solvers.

Parallel performance has been measured from a 3-dimensional flow simulation. The problem size is roughly 2.4 million mesh points due to the memory allocation limit on a sequential code. As presented in Figure 1, the speed-up ratio is linear (around 90% of parallel efficiency) at small number of cores and it is maintained around 20 with more processors, which shall be improved in the larger problem domain. We also observe that algorithmic changes on time evolution scheme and the reduction of boundary condition impositions on a baseline code will improve the parallel performance with the convergence criteria, which shall be main objectives of a next project.

This high-end user support provides the opportunity of possessing well-tuned application codes to domain scientists. It will accelerate the production of high-quality scientific researches. Meanwhile, this cooperation requires the sufficient number of application experts in individual scientific domain who is capable of dedicating this long-term service. It necessitates more financial support for incrementing application experts on various scientific domains.

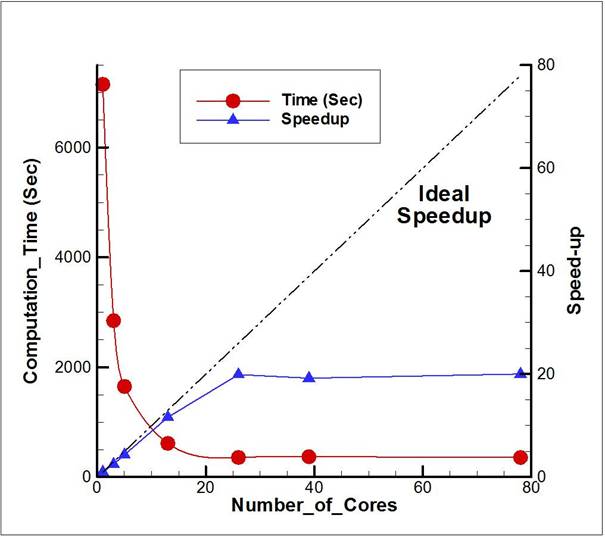
Figure 1 Computation Time and the Speed-up of a Parallelized LES Code